
Now in order to find the second moment of inertia: Using this we can find the first moment of inertia about the x-axis. The centroid of this elemental area from x-axis = y sin θģ. It is given as:ĪBCD is a sector with area = (r⋅d θ) ⋅ dr = r ⋅ drd θ Now we have to determine the differential area by finding the area of the element. Here in order to derive the moment of inertia of a semicircle we define the coordinates using the polar system. The macro-scale area density is given in this equation: dm/da= σĭerivation of Formula for Moment of Inertia of Semicircleġ. Area density (σ) is an intensive property, meaning that it does not depend on the amount of the material, and also as long as the mass is uniform, its area density is the same whether you have chosen the entire semicircle or a small strip of differential width. Use the concept for area density, which is mass divided by area. Add all of the individual strips using integral Calculus. Now writing an expression for the area density for the whole semicircle and then the tiny strips of differential widths. Selecting and defining a tiny strip of mass with differential width. M.O.I relative to the origin, Jo = Ix + Iy = ⅛ πr 4 + ⅛ πr 4 = ¼ πr 4 Now to find the moment of inertia of the semicircle we will take the sum of both the x and y-axis.
MOMENT OF INERTIA OF A CIRCLE WIRE FULL
Thus, M.O.I will be half the moment of inertia of that of a full circle. Here, the semi-circle rotating about an axis is symmetric, and therefore, we consider these values equal. Thus similarly for the semicircle, the moment of inertia of the x-axis is equal to that of the y-axis.
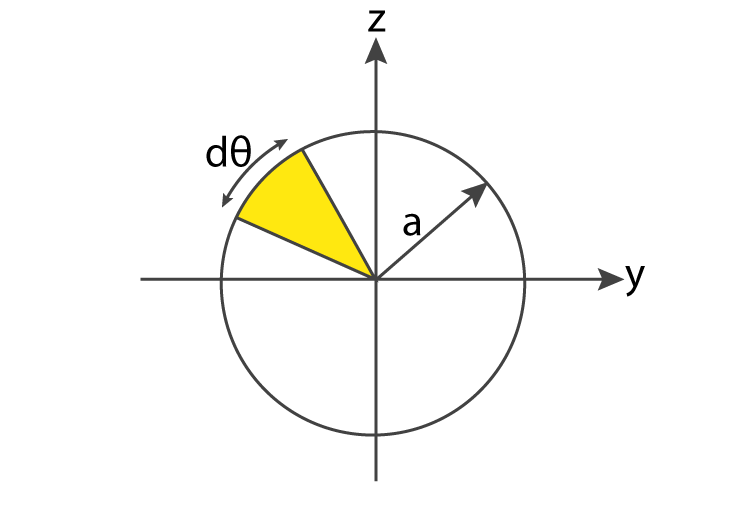
Now we need to pull out the area of a circle which gives us: M.O.I relative to the origin, Jo = Ix + Iy = ¼ πr 4 + ¼ πr 4 = ½ πr 4

We know that for a full circle because of complete symmetry and uniform area distribution, the moment of inertia relative to the x-axis is equal to that of the y-axis. Further to determine the moment of inertia of the semi-circle, we will take the sum of both the x and y-axis. The moment of inertia of the semicircle is generally expressed as I = πr 4 / 4.Here in order to find the value of the moment of inertia of a semicircle, we have to first derive the results of the moment of inertia full circle and basically divide it by two to get the required result of that moment of inertia for a semicircle. The moment of inertia of the semicircle is generally expressed as I = πr 4 / 4 Similarly larger the moment of inertia of the body more difficult is to stop its rotational motion. For example, if the body is at rest the larger the moment of inertia of the body the more difficult it is to put the body into the rotational motion. In other words, the moment of inertia is the measurement of resistance of the body to a change in its rotational motion. Once you have obtained the expression for MI, substitute r in terms of l given that the length of the wire forms the circumference, and to this end, arrive at the appropriate result.įormula used: Moment of inertia for a half-ring: $I = \dfrac$Īlso, remember that the moment of inertia is dependent on the distribution of mass of the system about the axis of rotation, the position and orientation of the axis of rotation and the shape of the body constituting the system.The moment of inertia plays the same role in rotational motion as the mass does in the translational motion. This will be an angular component of the radius of the semi-circle. Remember to consider the linear distance between the axis of rotation and the elementary mass while taking the distance of the elementary mass.

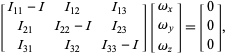
Then, obtain an expression for the elementary moment of inertia MI and integrate this over the entire angular span (0 to $\pi$) of the semi-circle. Hint: Begin by taking an elementary mass over the circumference of the semi-circle spanning an elementary angle of $\theta$.


 0 kommentar(er)
0 kommentar(er)
